602: Nearest Neighbour Classification and Regression
More than just similarities
- Classification: Predict the same class as the nearest observations
- Regression: Predict the same value as the nearest observations
???
Remember for classification tasks, we want to predict a class for a new observation.
What we could do is predict a class that is the same as the nearest neighbour. Simple!
For regression tasks, we need to predict a value. Again, we could use the value of the nearest neighbour! Simple again!
Nearest neighbour classification
Nearest neighbour regression
???
We’ve used the nearest neighbour in these examples to demonstrate the idea.
But in reality we don’t want to use a single neighbour. It could be noise.
Instead, we can use a weighting of some number of neighbours. For example in classification we would take predict the class which had the majority of nearest neighbours. For regression we might take the average value.
Equally, we could estimate the class probability by looking at the proportion of the nearest neighbours belonging to the predicted class.
(Beware of class probabilities on small numbers of observations!)
Generally, when we’re using more than one neighbour the name of the algorithm is shortened to k-NN.
Where k refers to the number of neighbours used in the algorithm.
In general, higher values of k perform more averaging and give “smoother” results.
Let’s take another look at the “iris” dataset with various values of k.
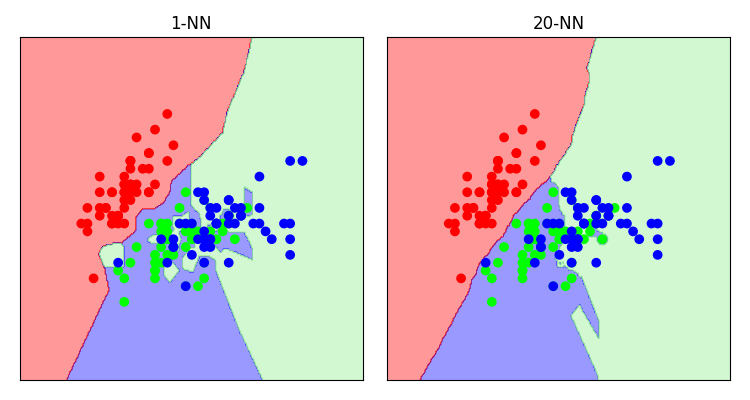
Bias and variance part duex
What we’re seeing here is overfitting and over-generalisation in practice.
By choosing low values of k we are highly sensitive to outliers. We overfit.
But choosing high values of k, the model might not be complex enough to represent the data.
How do we pick a value of k?
We saw before how to use validation to pick make sure we are not over or underfitting.
We can do the same here, by varying the value of k and validating the result.
But be careful of the choice of K. It should be…
- a coprime of number of classes and K
E.g. two classes, if we used a value for K of 6, we could have ties.
- greater or equal to the number of classes plus one
To give each class opportunity to have it’s say.
- High enough to avoid spurious results
- Low enough to avoid always picking the most common class
Pros/Cons
The pros of using k-NN are obvious and were stated at the beginning.
- The algorithm is very simple to understand.
- It is very flexible; you can use it for similarity matching, classification or regression.
- It is easy to tune; there’s often only a simple parameter.
However, there are issues. Of which we discuss next.
Justification
- How can you justify the result?
E.g.
“your mortgage application was declined because of your similarity to three people that defaulted, whom were also Danish”
- We’ve created a complex look-up table. It doesn’t improve our knowledge of the data.
???
First, and this doesn’t necessarily apply only to k-NN, how do you explain and justify the result?
Netflix justifies their k-NN recommendation by saying “you might like ‘I’m Alan Partridge’, because you liked both ‘Brass Eye’ and ‘Borat’”. And you’re probably ok with this justification.
But if you were declined a mortgage because “your application has been declined because your circumstances (where you live) were similar to those who have defaulted”. This might not be as easy to chew.
Furthermore, it is harder to learn something from the model, because we’re not actually modelling anything. We’ve basically created a sophisticated look up table. Stakeholders may not like this result.