501: Over and Underfitting
Generalisation and overfitting
“enough rope to hang yourself with”
- We can create classifiers that have a decision boundary of any shape.
Very easy to overfit the data.
This section is all about what overfitting is and why it is bad.
???
Speaking generally, we can create classifiers that correspond to any shape. We have so much flexibility that we could end up overfitting the data.
This is where chance data, data that is noise, is considered a valid part of the model.
In reality, we are interested in models that are able to generalise; models that are able to classify observations that have not been observed thus far.
Generalisation
Given some data, think of a simple way to accurately classify that data?
- Build a lookup table
Lookup tables cannot generalise to new examples.
Tip: Beware of 100%
???
Imagine we had a historical dataset of customers that did or did not click on a range of image based adverts. An advertising client has asked whether we can predict whether a customer would click on the advert.
- We go away and report back that we have 100% accuracy.
- We tell them that we have created a lookup table for every user for every advert.
- We have successfully classified all instances of whether a user will click on an advert.
Clearly this is a ridiculous example; we couldn’t claim that it predicted anything.
This is why we need to generalise our models, to cope with new data.
Overfitting
- Complex models produce lookup tables
Overfitting is the word used to describe when models are too complex.
E.g. Decision trees could create a decision rule for every observation.
Key point: Data Science is all about compromise
???
Despite the the previous example being so contrived, every ML algorithm has the capability of overfitting.
For example, decision trees can very easily create decision rules that segment every single piece of data.
And this occurs far more often than you might think.
The fundamental problem is that most real-life data is complex. We need complex models to cope with the complexity.
So there is a trade-off between how well we can model the problem and how much we overfit.
Why is overfitting bad?
- Noise
You don’t want your decision boundary to hug observations, because they are probably noisy.
???
All data is inherently noisy. Even the simplest of experiments contain noise.
Data with more features have compounding noise sources.
With more complex data it is very common to have noise that is not distributed according to a random process. For example, some data is missing, or invalid.
At best, we end up training our model on the noise, rather than the signal of interest.
At the worse, we could end up using spurious, factually incorrect data, to create our model.
Any new observations that arrive within these bounds will be classified incorrectly.
Underfitting
Underfitting is a lack of model complexity.
This usually occurs in domains where there are inherently large numbers of features, e.g. images.
2D example:

Spotting overfitting can be hard
- How do we visualise under/overfitting?
- It can be difficult.
Let’s look at an example using the make_circles data…
???
The problem with overfitting is that it is very hard to tell when you have overfitted. Especially when it’s hard to plot the features/decision surface (e.g. many features).
For example, using the make_circles data, let’s try and plot the accuracy of of a model vs a parameter…
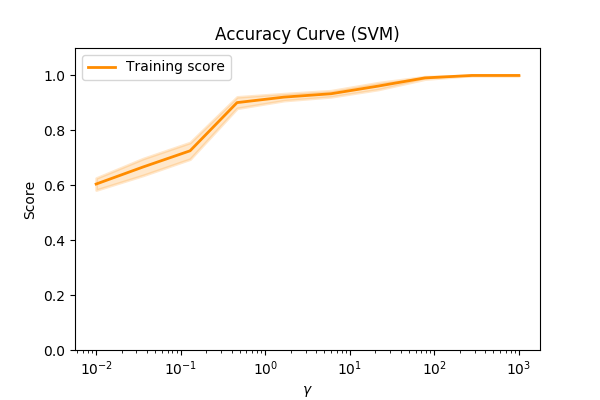
We can see that as we alter the value of \(\gamma\) the accuracy increases. We might assume that we have a better model.
But we would be wrong. Let’s look at a plot of the decision boundary (this isn’t usually possible due to the number of features!)…
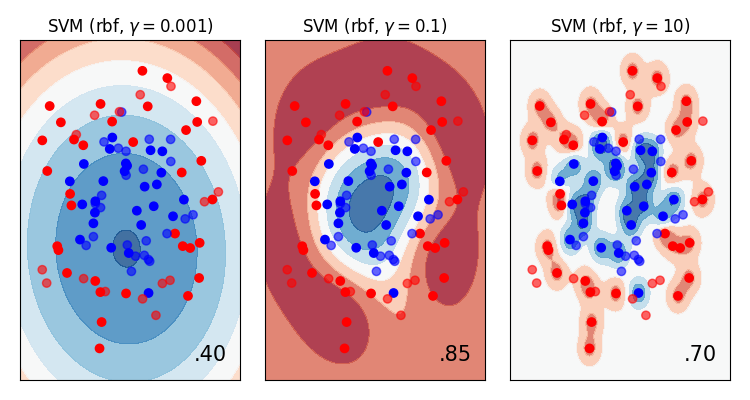
If we look at the right most plot, we can see that we are not generalising any more. We’re fitting too closely to the data. Essentially, we’ve created a very complex look-up table!
Let’s look at this over some more datasets…
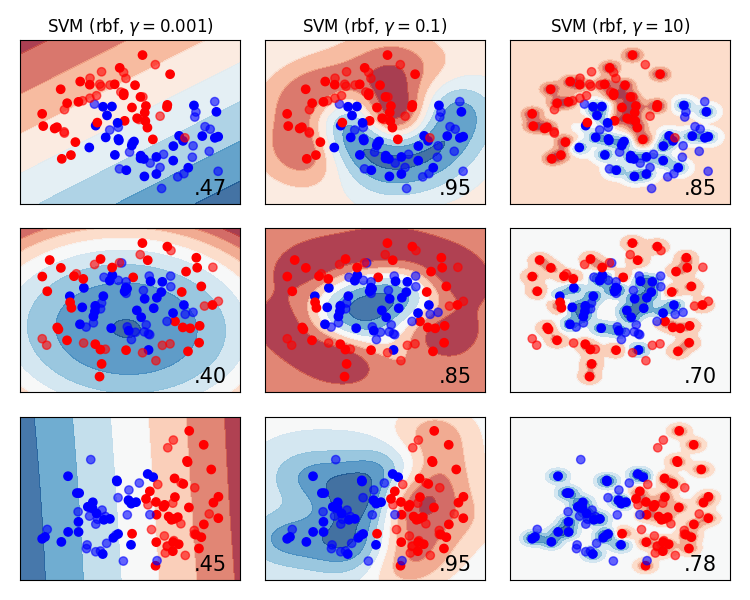
So how can we make sure that we don’t produce misleading scores?
This is probably the most important part of data science, so pay attention!
