404: Nonlinear, Linear Classification

Nonlinear functions

• Sometimes data cannot be separated by a simple threshold or linear boundary.

We can also use nonlinear functions as a decision boundary.

???

To represent more complex data, we can introduce nonlinearities. Before we do, bear in mind:

• More complex interactions between features yield solutions that overfit data; to compensate we will need more data.
• More complex solutions take a greater amount of computational power
• Anti-KISS

The simplest way of adding a nonlinearities is to add various permutations of the original features. For example, some feature squared.

Polynomial Features for Nonlinear Logistic Regression

1. Create new features, polynomials of the original data
2. Perform logistic regression using all of the new features

Still a linear classifier, we’re just using more complex features.

???

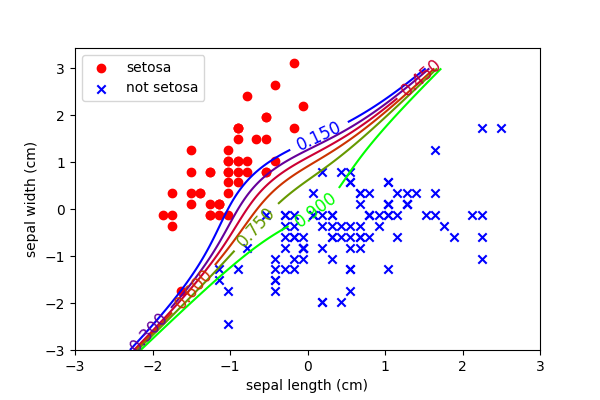
This is a logistic classifier with a polynomial expansion to a degree of 3. E.g. before we just had two features, \(x_1\) and \(x_2\). Now we have nine:

$$ x_1 + x_2 + x_1 x_2 + x_1^2 + x_2^2 + x_1^2 x_2 + x_1 x_2^2 + x^3 + x^3 $$

The beauty is that this is still a linear problem and therefore fast and guaranteed to optimise.

Nonlinear SVMs

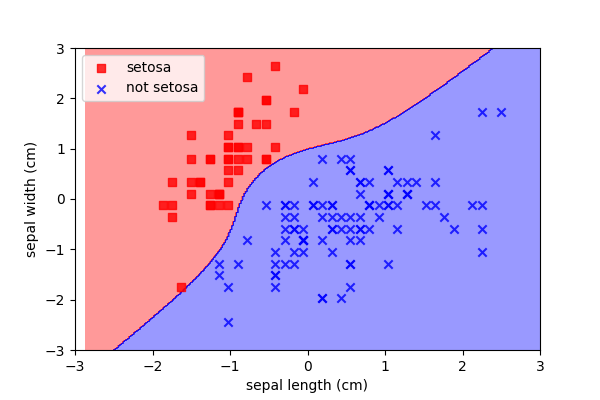
A similar polynomial trick can be performed with SVMs:

Kernel trick

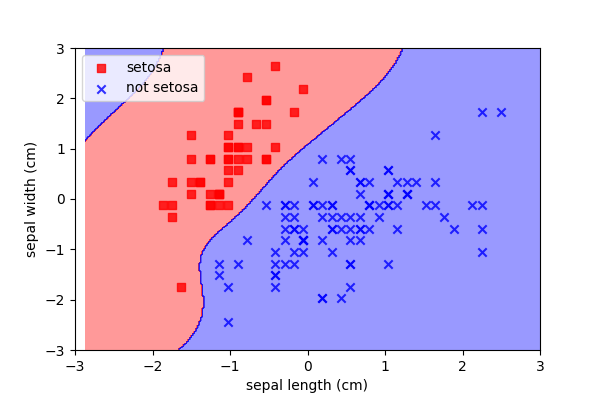
Briefly, one final strategy to note is called the kernel trick. Essentially this convolves a kernel (of any shape) over the data. This is a data transformation. We are mapping the data from one domain into another.

Schematic of Linear Classification

It’s sometimes easier to visualise an algorithm as a schematic or a graph.

For each of the linear classifiers, we ere altering the activation function.

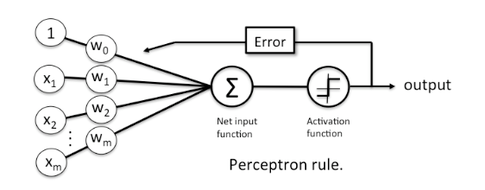
Key Point: This is actually an image of a Perceptron, the base unit in Neural Networks.

All of Deep Learning is based upon lots of linear classifiers!!!

???

Neural networks

The ultimate progression of nonlinear classifiers has resulted in stacked neural networks.

Neurons are fairly simple nonlinear classifiers. They are based upon a range of activation functions which are essentially cost functions for a single feature combination.

The functions are very familiar, with logistic-like, hinge-like and one-zero-like activation equivalents.

But the real advantage is that the neurons can be stacked in any number of formations to provide incredibly nonlinear functions.

Functions so nonlinear that they approach the capacity of the human brain in a number of specific domains (e.g. image classification).

A really hot topic, but bewilderingly huge. We delve into neural networks in the third workshop (advanced).