302: How to Engineer Features

Engineering features

You want to do this because:

• Reduces the number of features without losing information
• Better features than the original
• Make data more suitable for training

???

Another part of the data wrangling challenge is to create better features from current ones.

Distribution/Model specific rescaling

Most models expect normally distributed data. If you can, transform the data to be normal.

• Infer the distribution from the histogram (and confirm by fitting distributions)

• Apply the inverse transformation to re-normalise

Some example types of data that follow these distributions:

• natural-log: The length of comments posted in Internet discussion forums
• natural-log: Time to repair a maintainable system
• power-law: The Severity of violence
• power-law: The relationship between a CPU’s cache size and the number of cache misses

???

We touched upon this earlier, but you may be able to transform the data directly into normally distributed data.

Very common in physical problems, log scaling is required in situations where the underlying process is affected by a power law (e.g. exponential growth in y for a linear increase in x).

You may ask “how am I supposed to know that!?”. This is where domain knowledge comes into play. But most often these things are most obvious when plotting the histogram.

Other types of scaling include: square, square root, natural-log.

Some example types of data that follow these distributions:

• natural-log: The length of comments posted in Internet discussion forums
• natural-log: Time to repair a maintainable system
• power-law: The Severity of violence
• power-law: The relationship between a CPU’s cache size and the number of cache misses

Data affected by a power law (exponential distribution):

Data affected by a natural logarithm (log-normal distribution):

Combining features

• Many domains have already encoded important combinations of features:
  • velocity, body mass index, price-earnings ratio, queries per second, etc.

Looking for new combinations can be lucrative.

???

Rescaling has become a standard pre-processing technique in data science. But feature combination is less prevalent; presumably because it requires some domain knowledge.

But this is at odds with the rest of the world, because there are many, many examples of combined features being used in everyday life: velocity, body mass index, price-earnings ratio, queries per second, etc.

For domain experts, many of these types of features may be known. However, looking for new combinations or transformations can be lucrative.

Types of combinations

• Multiplication or division (ratio)
• Change over time, or rate
• Subtraction of a baseline
• Normalisation: Normalising one variable with respect to another. E.g. the number of failures in itself is probably not that useful. However a failure rate as a percentage could be very useful. (i.e. number of failures / total requests)

???

There are many ways in which to combine features, but these are the most common:

When creating new variables, always bear in mind the goal. The purpose of creating new features is to provide new information that make the goal easier to achieve.

Example: Polynomial features

sklearn provides us with one easy feature generation method called PolynomialFeatures.

This gnerates high-order interaction terms with each of the features. For example, the dataset:

$$ \mathbf{X} = \left[X_a, X_b\right] $$

becomes:

$$ \mathbf{X_p} = \left[X_a, X_b, X_a \times X_b, X_a^2, X_b^2, \dots \right] $$

???

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   0.,   0.,   1.],
       [  1.,   2.,   3.,   4.,   6.,   9.],
       [  1.,   4.,   5.,  16.,  20.,  25.]])

Feature Selection

Tip: Minimise the number of features

But how do we select which features to use?

???

The problem with generating lots of features is that this increases the changes of overfitting (which we will discuss in the next section). To mitigate this we want to reduce the number of features.

Assuming we’re not domain experts quite yet (or even if we are), how do we decide which features to include in our training dataset?

How can we tell which features are the most important given our goal?

In the previous section we saw a technique to partition data based upon information gain. We will see this again soon…

Correlation

Correlating features in datasets are bad.

• Algorithms think that duplicate information represents importance
• Correlating features don’t add any more information

???

Recap: Correlation is a measure of the statistical dependence between two quantities. I.e. if one features changes, does another feature change in lock-step?

At worst, the feature doesn’t add any more information. We can obtain the same amount of information from one feature alone.

In reality, correlating features tend to reduce performance due to the optimisation problem we saw in the scaling section. The optimisation function will expend effort trying to optimise these redundant variables.

At best, it will simply take a lot longer to reach the same result (this is only true for “sparse” optimisers - those that penalise large numbers of features).

At worst, the model will start overfitting because of the extra features (i.e. because you have two features saying the same thing, that must be REALLY important!)

This is a plot of the Pearson Correlation Coefficient for different 2D datasets. The datasets with a coefficient near 1 or -1 are highly correlated and will affect the performance of your model.

When features do correlate with each other, they are said to be collinear. I.e. they are linearly dependent on each other.

When comparing the colinearity between all features (i.e. first with second, first with third, etc.) this is called testing for multicollinearity.

• Simple: visualise the data
• Automated: Inspect the eigenvalues of the correlation matrix.

???

Eigenvector Analysis

Our goal is to pick features that do not correlate. (remember the 2D plot here).

Hence, if we look for very low eigenvalues, this tells us exactly which features have highly correlating features.

Once we know which features are correlating we can look at the eigenvector for that eigenvalue to show us which of the features it correlated with!

This is a bit complex, so let’s look at a concrete example…

Example: Correlating features

X = np.random.randn(100,5)
noise = np.random.randn(100)
X[:,0] = 2*X[:,2] + 3*X[:, 4] + 0.5*noise

Let’s calculate the correlation, then the eigenvalues for this correlation matrix:

corr = np.corrcoef(X, rowvar=0)
w, v = np.linalg.eig(corr)
print('Eigenvalues of features in X')
print(w)

Eigenvalues of features in X
[ 2.13215129  0.00826567  1.20093744  0.97602299  0.68262261]

Here, we have an low valued eigenvalue. This is saying, in one of the feature combinations, there is little variance (i.e. little information).

Note that the order of the eigenvalues is not guaranteed; it does not represent a feature.

Now, let’s view the eigenvectors for that eigenvalue…

print('Eigenvector for eigenvalue 1')
print(v[:, 1])

Eigenvector for eigenvalue 1
[ 0.72545976 -0.00837951 -0.37350552  0.00075081 -0.57804064]

This array is stating that the direction in which we have little variance is in the 0th, 2nd and 4th features. (remember the eigenvector is the axis that skewers the data in a direction).

So, we need to remove either one (or more) of these features.

(Probably the first, since that appears to have the largest correlation with the other two)…

corr = np.corrcoef(X[:,1:], rowvar=0)
w, v = np.linalg.eig(corr)
print('Eigenvalues of features in X')
print(w)

Eigenvalues of features in X
[ 0.68138777  0.92924905  1.25915791  1.13020527]

No more correlating features!

Example: Correlating features

X = np.random.randn(100,5)
noise = np.random.randn(100)
X[:,0] = 2*X[:,2] + 3*X[:, 4] + 0.5*noise

class: center, middle

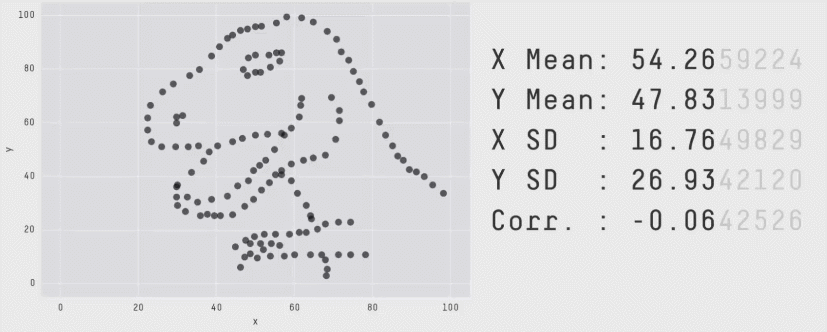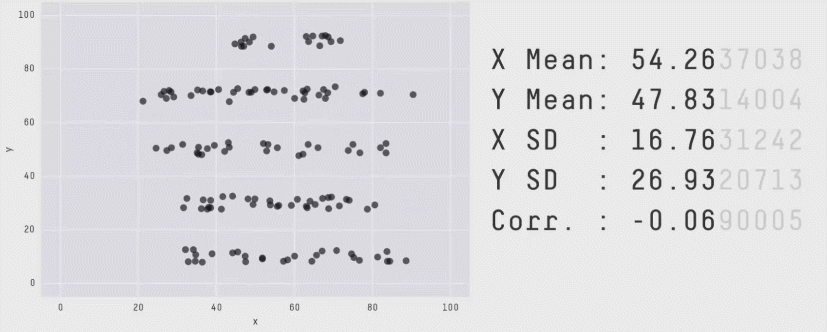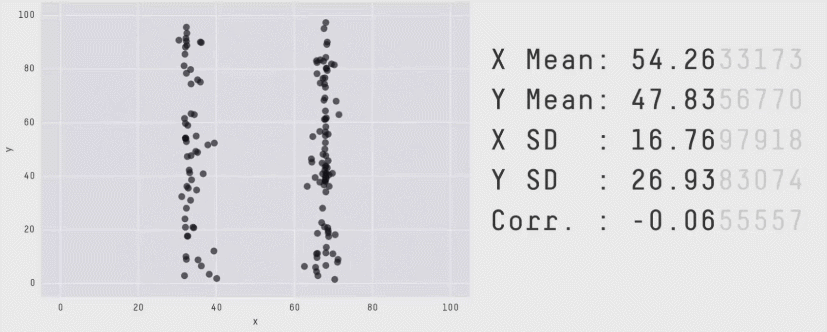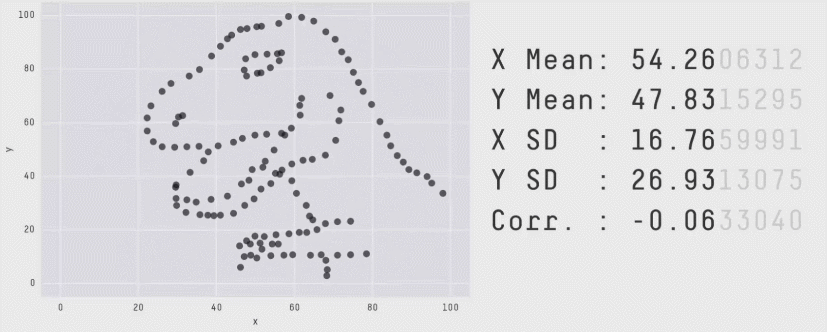
Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing - Justin Matejka, George Fitzmaurice

Feature importance

Two general ways to infer importance:

• Brute force: test your model performance using different combinations of features
• Infer importance from another type of score

???

After we’ve removed correlating features, we’re well on out way to defining the most informative features.

However, how can we tell which features are the most important?

One way is to use a single feature to generate a score. The features that generate the highest scores can be said to be the most informative.

sklearn has one dedicated method using trees…

Feature importance with trees

We’ve just touched upon one type of classification/regression algorithm, decision trees.

We saw that the tree attempts to segment the data by increasing the purity of the classes.

Remember that trees build up their segmentation tree agglomeratively. I.e. highest levels in the tree make the broadest decisions. We can then say that the highest levels of the tree are the most informative.

Example: feature importance with random forests

Finally, we can’t rely on one decision tree. Decision trees tend to overfit data. What we can do is to create lots of trees, and randomise the data going into each tree. This gives us some statistical estimate of how stable the feature importance is.

Let’s give this a try on some synthetic data…

# Build a classification task using 3 informative features
X, y = make_classification(n_samples=1000,
                           n_features=10,
                           ...

# Build a forest and compute the feature importances
forest = ExtraTreesClassifier(n_estimators=250,
                              random_state=0)

forest.fit(X, y)
importances = forest.feature_importances_
std = np.std([tree.feature_importances_ for tree in forest.estimators_],
             axis=0)
indices = np.argsort(importances)[::-1]

# Print the feature ranking
print("Feature ranking:")

for f in range(X.shape[1]):
    print("%d. feature %d (%f)" % (f + 1, indices[f], importances[indices[f]]))

# Plot the feature importances of the forest
...

Feature ranking:
1. feature 1 (0.295902)
2. feature 2 (0.208351)
3. feature 0 (0.177632)
4. feature 3 (0.047121)
5. feature 6 (0.046303)
6. feature 8 (0.046013)
7. feature 7 (0.045575)
8. feature 4 (0.044614)
9. feature 9 (0.044577)
10. feature 5 (0.043912)

Note that the information gain does not represent how “important” each feature is.

Just how well we can separate classes with simple rules.

???

The y-axis can be interpreted as the proportion of importance over the classification in the dataset.

It does not represent how much the feature “explains the data”. The scores are simply a ratio of the numbers of classifications that were made when using that feature alone.

One caveat is related to the implementation of the tree optimisation. Tree algorithms pick the next best feature to segment the data. This means that if there are correlating features, only one will be used to segment the data, since once segmented, the same correlating feature will not produce any purer classes.

The result is that of the correlating features, only one will be shown as important. The others will be ranked as not important because they are not used.

Another caveat worth mentioning is the choice of score being used in the tree algorithm. Because we’re aiming to promote more informative features, we should chose a score that is based on a measure of information; i.e. entropy.

However, if the goal is to produce better separating classes, then consider using gini metric.

Sequential feature selection

1. Iteratively add or remove features whilst measuring performance.

2. Remove features that don’t improve performance

Pros:

• Related to your chosen performance metric

Cons:

• Computationally expensive

???

A similar method of choosing features is to iteratively add or remove features from a dataset and recompute the score.

For example, if we had the iris dataset with three features, we would start by testing each feature as a classifier. We would pick the best scoring feature and use that as our “single feature” score.

Next, we would use the first feature and concatenate a second feature from the remaining two. Again the best combination will be saved as the best “two feature” score.

And so on.

We could then make a choice to remove features that were not increasing the score significantly.

This algorithm isn’t difficult to code, but is not available in sklearn.

The next best recommended library for implementing this is the mlxtend library: https://github.com/rasbt/mlxtend. It’s also got some handy plotting functions.

Sparse models through regularisation

• Some models can automatically penalise features
• They do this by setting feature weights to zero
• Robust, because it is within the context of the model

Still remove features manually. It improves understanding and computational efficiency.

???

One final thing I want to mention is sparse regularisation inside the learning algorithms.

Some algorithms implement regularisation, which is the act of penalising the use of large numbers of features in the model.

This is a very robust method of removing uninformative features, because they are removing them within the context of the model.

For example, features selected by a decision tree (a simple, linear thresholding like algorithm) might not choose the best features for a highly complex nonlinear deep learning algorithm that is capable of extraordinary combinations of features.

However, in my experience it is certainly worth trying to remove very uninformative and correlating features, purely to reduce the computation load of having lots of features.

If you can get it down to two or three dimensions, then this helps with plotting too.

Obtaining data

I was going to talk about how to get data. But the reality is that it depends entirely on the domain that you are working in.

There are a huge amount of test and dummy datasets available freely on the internet and you can get access to streaming data from the likes of twitter, etc.

But the reality is that it depends entirely on your problem.

From my experience, the most valuable data is proprietary, and specific to the business. These are the types of data that tend to produce the most valuable outcomes.

For everything else, search for it.